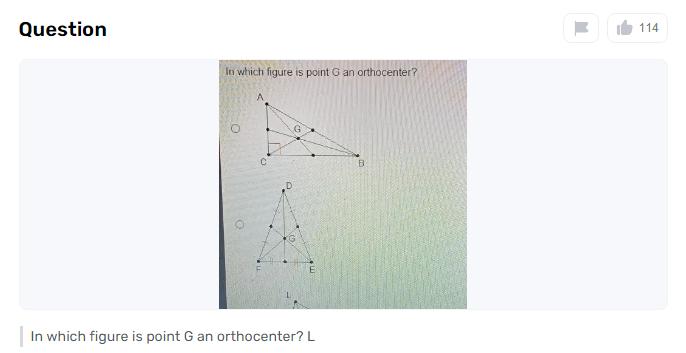
Geometry can be a confusing maze of angles and shapes. The fascinating idea of the orthocenter, or the intersection of a triangle’s elevations, is the focus of this investigation. In any case, how would we recognize a figure where a particular point, similar to point G, addresses the orthocenter?
This article divulges the key qualities that recognize triangles with orthocenters at point G. We will equip you with the knowledge to confidently identify in which figure is point g an orthocenter? and navigate the complexities of triangle geometry by examining clues like the location of G, inside or outside the triangle, and the relationship between the altitudes.
What does Orthocenter Mean?
The orthocenter, also known as H, is a critical point in a triangle in the field of geometry. Envision three lines, called heights, each drawn opposite from a vertex to the contrary side of a triangle. The supernatural convergence point of these heights is definitively the orthocenter.
This point doesn’t necessarily in every case live inside the actual triangle, and its area can uncover fascinating properties about the triangle’s shape and qualities. We can delve deeper into the fascinating world of triangles and their hidden secrets with the help of an understanding of the orthocenter.
Steps to Identify the Orthocenter
Locating the orthocenter can be a thrilling detective story that requires a strategic approach and a keen eye. In this section, we begin a methodical journey to locate this elusive point:
Building the Altitudes
The construction of the altitudes themselves serves as the foundation for our investigation. Consider each of the triangle’s vertex as a suspect and the opposing side as their defense. The elevation goes about as the denouncing observer – a line section drawn oppositely from the vertex, meaning to uncover any disparities in the triangle’s construction.
Our reliable tools are a ruler and a protractor, which we use to make sure these lines meet at a perfect 90-degree angle so there is no room for doubt.
Extending the Lines
However, our investigation does not end at the triangle’s base. Very much like a decided criminal investigator wouldn’t leave a lead partially through, we expand every height past the place of convergence. Envision these lines as expanded cross-examination meetings, testing further into the triangle’s privileged insights. We imagine them proceeding with vastly in the two headings, similar to strings extending towards an obscure response.
The Intersecting Point
Our investigation comes to a close at the convergence point. Here, where each of the three expanded elevation lines meet, lies the much-sought-after orthocenter. This place of convergence, no matter what its area inside the triangle’s limits or hiding outside, is the response we’ve been looking for. It symbolizes the location where the “crimes” of unbalanced triangles and non-perpendicular lines are made clear.
Shortcut Techniques for the Astute Detective
There may be a way to identify the orthocenter without extending each line for the truly perceptive detective. Certain triangle types offer significant hints:
The Right Point’s Tell
For a right triangle, the orthocenter helpfully uncovers itself at the vertex where the right point lives. No requirement for broad addressing – the guilty party is discovered in the act!
An Instance of Symmetry
In an isosceles triangle where different sides are indistinguishable twins, the elevation drawn from the vertex where these sides meet corresponds with the middle bisecting the base. This demonstrates the obvious case of following the money trail by revealing the orthocenter’s location right on that line!
Affirmation Through Proof
Whenever we’ve distinguished a possible area for the orthocenter, a careful investigator wouldn’t rest without substantial proof. The methods for confirming are provided by geometry. For example, in an intense triangle, where all points are under 90 degrees, the orthocenter lives inside the actual triangle.
Additionally, the triangle is divided into two areas by each altitude in a particular ratio, typically 1:2 or 2:1. Counseling laid out mathematical hypotheses connected with orthocenters can give the last blessing, setting our derivation.
How to Use Gauth for Mathematical Questions
Feeling lost in a labyrinth of numerical conditions? Gauth can be your signal, directing you towards understanding and arrangements. This is a breakdown en route to use this incredible asset really:
Step 1. Open Gauth
Open the app or website for Gauth. It invites you with a perfect connection point, prepared to handle your numerical misfortunes.
Step 2. Enter Your Math Question Here
The magic starts here! There are two choices. In the designated text box, clearly state your question. Be specific; Gauth will be able to better comprehend your requirements the more information you provide. Stayed with a perplexing condition or chart? Don’t worry about it! Gauth permits you to transfer an image of your concern utilizing your telephone’s camera or by choosing a current picture from your gadget.
Step 3. Let Gauth Analyze
Simply click the submit button after entering your question to allow Gauth to perform its AI-powered analysis. It will look at your question, figure out the mathematical ideas involved, and use its extensive knowledge base to find the best answer.
Step 4. See the Answer
In practically no time, Gauth presents the solution to your inquiry. However, it does not end there! It aims to give students a full learning experience. You’ll see an unmistakable bit-by-bit breakdown of the arrangement cycle, analyzing each step into justifiable parts.
Ending Remarks
Understanding the type of triangle and accurately drawing the altitudes are necessary for locating the orthocenter. The orthocenter’s position changes with intense, harsh, and right triangles, being inside, outside, or at the vertex of the right point, separately. By following these means, you can decide the figure where point G is the orthocenter that improves comprehension you might interpret triangle properties and mathematical developments.